BESARAN VEKTOR
Assalamau’alaikum Sahabat!!! Bagaimana kabar kalian hari ini?
Semoga dalam keadaan sehat selalu ya, Aamiin Yaa Allah
Pada kesempatan ini, skuyberbagi membahas tentang besaran dalam
segi ada tidaknya arah. Namun, kali ini skuyberbagi hanya akan lebih membahas
Besara Vektor dibanding dengan Besaran Skalar kepada teman-teman skuyberbagi
sekalian. Untuk itu, simak baik-baik ya.
A.
Pendahuluan
Besaran adalah segala sesuatu yang dapat diukur dan dinyatakan
dalam bentuk angka-angka. Besaran di dalam fisika dibagi menjadi besaran pokok
dan besaran turunan. Besaran pokok adalah besaran yang standar. Sedangkan besaran
turunan merupakan penurunan dari besaran-besaran pokok.
Untuk membedakan suatu besaran apakah skalar atau vektor maka
dibuatlah sebuah aturan yaitu:
Notasi yang diketik dengan huruf dengan tanda panah di atas
menandakan bahwa besaran tersebut adalah besaran vektor. Contoh untuk vektor
kecepatan dinotasikan dengan notasi (V) dengan tanda panah (→) di
atasnya, sementara jika notasi tanpa tanda panah (V) dan dengan menggunakan huruf biasa
(regular) maka yang dimaksudkan adalah besaran skalar. Penulisan lain untuk
skalar adalah dengan menggunakan tanda mutlak |V|. Sementara dalam
pengetikan, notasi dengan menggunakan huruf tebal (bold) adalah notasi untuk menandakan vektor, misalnya V.
Dalam segi ada tidaknya arah, besaran dibagi menjadi besaran skalar
dan besaran vektor.
a.
Besaran Skalar
Pada saat menghitung luas sebuah bidang bujur sangkar, maka kita
hanya menyebut angka (nilai) nya saja, misalkan 25 cm2. Demikian pula
pada saat kita membeli dan menimbang satu keranjang buah mangga, maka pada
timbangan tertera angka yang menunjukan massa dari mangga tersebut, misalkan 4
kg.
Dari contoh diatas kita bisa mengambil kesimpulan bahwa luas dan
juga massa termasuk ke dalam besaran vektor. Besaran vektor yaitu besaran
yang hanya memiliki nilai (magnitude) dan tidak memiliki arah. Berikut adalah
besaran yang termasuk ke dalam besaran skalar:
No.
|
Besaran Skalar
|
Lambang Besaran
|
Satuan
|
Lambang Satuan
|
1.
|
Panjang
|
Ɩ
|
Meter
|
m
|
2.
|
Massa
|
m
|
Kilogram
|
Kg
|
3.
|
Jarak
|
s
|
Meter
|
M
|
4.
|
Kelajuan
|
v
|
Meter per sekon
|
m/s
|
5.
|
Volume
|
V
|
Meter kubik
|
m3
|
6.
|
Waktu
|
t
|
Sekon
|
S
|
7.
|
Jumlah mol zat
|
N
|
Mole
|
mol
|
8.
|
Intensitas cahaya
|
J
|
Kandela
|
cd
|
9.
|
Energi
|
E
|
Joule
|
J
|
10.
|
Usaha
|
W
|
Joule
|
J
|
11.
|
Daya
|
P
|
Watt
|
W
|
12.
|
Massa jenis
|
ρ
|
Kilogram per meter kubik
|
Kg/m3
|
13.
|
Kalor
|
Q
|
Joule
|
J
|
14.
|
Kuat arus listrik
|
I
|
Ampere
|
A
|
15.
|
Suhu
|
T
|
Kelvin
|
K
|
b.
Besaran Vektor
Besaran vektor adalah besaran
yang memiliki nilai dan arah. Artinya, nilai dari besaran itu ditentukan arah. Contoh
dari besaran vektor adalah:
No.
|
Besaran Vektor
|
Lambang Besaran
|
Satuan
|
Lambang Satuan
|
1.
|
Perpindahan
|
Δs
|
Meter
|
M
|
2.
|
Berat
|
W
|
Newton
|
N
|
3.
|
Kecepatan
|
v
|
Meter per sekon
|
m/s
|
4.
|
Percepatan
|
a
|
Meter per sekon kuadrat
|
m/s2
|
5.
|
Percepatan gravitasi
|
g
|
Meter per sekon kuadrat
|
m/s2
|
6.
|
Momentum
|
m
|
Kilogram meter per sekon
|
Kg m/s
|
7.
|
Impuls
|
I
|
Newton sekon
|
Ns
|
8.
|
Gaya
|
F
|
Newton
|
N
|
9.
|
Tekanan
|
P
|
Pascal
|
Pa
|
10.
|
Momen gaya
|
τ
|
Newton meter
|
Nm
|
11.
|
Tegangan permukaan
|
y
|
Newton per meter
|
N/m
|
12.
|
Gaya gesek
|
Fg
|
Newton
|
N
|
13.
|
Induksi magnetik
|
B
|
Weber per meter kuadrat
|
Wb/m2
|
14.
|
Kuat medan gravitasi
|
F
|
Newton
|
N
|
15.
|
Kuat medan listrik
|
E
|
Newton per coulomb
|
N/C
|
B.
Macam-macam Vektor
Dalam ilmu fisika, terdapat dua macam besaran vektor, yaitu vektor
sejajar dan vektor berlawanan.
a.
Vektor
sejajar
Adalah dua vektor atau lebih yang memiliki arah serta besar yang
sama.
b.
Vektor
berlawanan
Adalah dua atau leih vektor yang memiliki besar yang sama namun
arahnya berlawanan.
C.
Jenis-jenis Vektor
Ada beberapa jenis vektor khusus yaitu:
a.
Vektor
posisi
Suatu vektor yang posisi titik awalnya di titik 0 (0,0) dan titik
ujungnya di A (a1 , a2).
b.
Vektor
Nol
Suatu vektor yang panjangnya nol dan dinotasikan dengan angka nol
(0) dengan garis di atasnya. Vektor nol tidak memiliki arah vektor yang jelas.
c.
Vektor
satuan
Suatu vektor yang panjangnya satu satuan.
d.
Vektor
basis
Vektor basis merupakan vektor satuan yang saling tegak lurus. Dalam
vektor dua dimensi (R2) memiliki dua vektor basis. Sedangkan dalam
tiga dimensi (R3) memiliki tiga vektor basis.
D.
Sifat-sifat Vektor
Vektor mempunyai sifat-sifat antara lain:
a.
Dapat
dipindahkan dengan syarat nilai atau besar serta arahnya itu tidak berubah;
b.
Dapat
dijumlahkan;
c.
Dapat
dikurangkan;
d.
Dapat
diuraikan;
e.
Dapat
dikalikan.
E.
Operasi Pada Vektor
a.
Penjumlahan
vektor
Penjumlahan vektor memuat rumus mencari resultan gaya yang
dijumlahkan. Dua buah vektor yang dinyatakan melalui anak panah akan membentuk
sudut. Selain nilai atau koordinat dari kedua vektor, besar sudut juga akan
mempengaruhi besar jumlah resultan vektor. perhatikan gambar di bawah.
Rumus mencari jumlah resultan dua buah vektor dinyatakan melalui
persamaan di bawah.
R2 = A2 + B2 + 2AB · cosα
Atau:
A/sinα = B/sinβ = C/sinγ
Pengurangan vektor memuat rumus mencari resultan gaya yang menjadi
selisih dari keduanya. Seperti halnya pada penjumlahan vektor, dua buah vektor
yang dinyatakan melalui anak panah dalam pengurangan vektor juga akan membentuk
sudut. Besar sudut tersebut akan mempengaruhi besar selisih resultan vektor.
perhatikan gambar di bawah.
Rumus pengurangan vektor dinyatakan melalui persamaan:
R2 = A2 + B2 – 2AB · cosα
c.
Perkalian
vektor
Ada dua cara yang bisa dilakukan dalam perkalian vektor, yaitu
perkalian cross dan perkalian dot.
1.
Perkalian
Cross
Persamaan untuk perkalian cross diberikan pada persamaan:
Keterangan:
|A x B| = hasil besar vektor dari perkalian silang vektor A dengan vektor B
α = sudut yang terbentuk pada vektor A dengan vektor B, dimana 0⁰ ≤ α ≤ 180⁰
|A x B| = hasil besar vektor dari perkalian silang vektor A dengan vektor B
α = sudut yang terbentuk pada vektor A dengan vektor B, dimana 0⁰ ≤ α ≤ 180⁰
2.
Perkalian
Dot
Persamaan untuk perkalian dot diberikan pada persamaan:
A · B = |A| |B| · cosα
Keterangan:
A = |A| ialah besar vektor pada A
A = |A| ialah besar vektor pada A
B = |B| ialah besar vektor pada B
α = sudut yang terbentuk pada vektor A dengan vektor B,
dimana 0⁰ ≤ α ≤ 180⁰
Perkalian titik dilambangkan dengan
tanda titik atau dot product (.). Macam perkalian vektor ini menghasilkan
skalar. Untuk itu perkalian titik juga dapat dinamakan dengan perkalian scalar
product. Dalam perkalian ini terdapat beberapa hal penting yang harus
diperhatikan seperti:
1).
A ·
B = 0 → cos 90⁰ = 0, apabila vektor A tegak lurus dengan vektor B sehingga
nilai α = 90⁰.
2).
A ·
B = AB → cos 0⁰ = 1, apabila vektor A searah dengan vektor B sehingga nilai
α = 0⁰.
3).
A ·
B = -AB → cos 180⁰ = -1, apabila vektor A berlawanan arah dengan vektor B
sehingga nilai α = 180⁰.
Sebuah vektor itu dapat kita
gambarkan dengan sebuah anak panah (→) yang terdiri atas pangkal, panjang dan
arah anak panah. Perhatikan gambar contoh vektor dibawah berikut ini:
Seperti anak panah pada gambar
diatas, pangkal anak panah tersebut menunjukkan sebuah titik tangkap (titik
awal) dari sebuah vektor, panjang anak panah tersebut mewakili besar atau suatu
nilai vektor (semakin panjang anak panah maka akan semakin besar pula nilai
atau harga vektor, begitu juga sebaliknya), sedangkan pada arah anak panah akan
menunjukkan arah vektor.
Untuk dapat lebih jelas tentang cara menggambarkan vektor, maka silahkan mari kita perhatikan contoh gambar vektor di bawah berikut ini:
Untuk dapat lebih jelas tentang cara menggambarkan vektor, maka silahkan mari kita perhatikan contoh gambar vektor di bawah berikut ini:
a.
(a) menunjukkan sebuah vektor
gaya F dengan sebesar 5 N ke arah kanan
b.
(b) menunjukkan sebuah vektor
gaya F dengan sebesar 10 N ke arah kiri.
G.
Cara Menggambarkan Resultan Vektor
Sebuah vektor
terdiri dari titik pangkal (tangkap) dan titik ujung (terminus). Panjang garing
sama dengan besar vektor dan arah panah menunjukan arah vektor. pindahkan titik
pangkal vektor kedua (B) pada titik ujung vektor pertama (A)
dengan tetap mempertahankan panjang dan arahnya. Lalu hubungkan titik pangkal
vektor pertama (A) dan titik ujung vektor kedua (B). Vektor
resultan (R) akan berpangkal pada titik pangkal vektor pertama (A)
dan bertitik ujung pada titik ujung vektor kedua (B).
Secara grafis
terdapat dua cara, yaitu metode poligon dan metode jajar genjang.
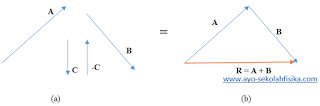
Metode segitiga
hanya untuk dua vektor (akan berbentuk segitiga) dan metode poligon untuk tiga
atau lebih vektor. tetapi cara menggambar untuk keduanya sama yaitu dengan
menghubungkan pangkal vektor dengan ujung vektor sebelumnya untuk semua vektor
yang akan dijumlahkan atau dikurangkan dan vektor resultannya adalah panah yang
ditarik dari pangkal vektor pertama ke ujung vektor terakhir.
Pada metode
jajar genjang, vektor-vektor yang akan dijumlahkan ditarik dari satu pangkal
yang sama dari berbentuk jajar genjang.
Secara analitis (perhitungan), yaitu:
a.
Jika
arah vektornya sama
Resultan vektor
yang memiliki arah yang sama dapat langsung dihitung dengan cara menjumlahkan
besar dari masing-masing vektor yang digabungkan.
R = V1 +
V2
b.
Jika
arah vektornya berlawanan
Resultan vektor
yang memiliki arah saling berlawanan dihitung dengan cara mencari selisih nilai
dari kedua vektor yang digabungkan.
R = V1 -
V2
c.
Jika
vektornya berbentuk sudut tertentu
Resultan atau
jumlah dari vektor yang arah vektornya membentuk sebuah sudut tertentu dapat
dicari menggunakan rumus.
R = √v12
+ v22 + 2v1v2 cosα







sudah baik, jangan lupa cantumkan sumber referensi ya.
BalasHapus